Fibonacci Spiral

Posted on Mar 28, 2010 in Code Sketches

I am fascinated by the Fibonacci (Golden) Spiral, and love the geometric construction, which is mimicked and expanded in this Processing sketch.

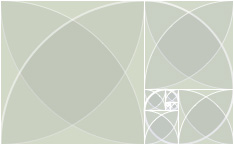
Fibonacci Spiral by Nathan Selikoff. 2010. Image capture from Processing sketch.

While developing an earlier concept for my website redesign, I created this version of the Fibonacci Spiral, with subtle coloration and fading arcs and squares.

// large version
// second attempt at a fibonacci spiral
// first attempt was great, but used rotation,
// which is expensive and imprecise
// here's the beginning of the fibonacci sequence...
// 0, 1, 1, 2, 3, 5, 8

void setup() {
  size(611, 378);
  smooth();
  frameRate(30);
}

int[] s = new int[3];
int tmp, phase;
float speed;

void draw() {
  // clear the screen to a nice green
  background(228, 236, 215);

  // initialize variables
  s[0] = 0;
  s[1] = 0; // first number of the fibonacci sequence
  s[2] = 1; // second number of the fibonacci sequence
  phase = 0; // simple counter; use this to apply fx to the boxes linearly
  speed = 0.01; // speed of the effects

  // set the origin at the end of the spiral
  translate(442, 272);

  // flip vertically to match my logo
  scale(1.0, -1.0);

  rotate(PI);

  // this loop constructs the spiral
  // basically, draw a square of side s, rotate 90deg, calculate the new s0 and s,
  // move up s0 + s, and repeat...
  while (s[2] < 611) {

    // use a sin function to give us some nice undulating effects
    float wave = sin((frameCount + phase*20) * speed) + 1.0;

    // styles for the arcs
    fill(0, 0, wave * 64, 10); // undulating transparent black fill
    stroke(255, wave * 255); // undulating white stroke

    // draw the quarter-circles inside the squares
    // set the stroke weight to 2 for the arc that makes the spiral
    if (phase % 4 == 0) strokeWeight(2); else strokeWeight(1);
    arc(s[2], s[2], 2*s[2], 2*s[2], PI, 3*PI/2.0);
    if (phase % 4 == 1) strokeWeight(2); else strokeWeight(1);
    arc(0, s[2], 2*s[2], 2*s[2], -PI/2.0, 0);
    if (phase % 4 == 2) strokeWeight(2); else strokeWeight(1);
    arc(0, 0, 2*s[2], 2*s[2], 0, PI/2.0);
    if (phase % 4 == 3) strokeWeight(2); else strokeWeight(1);
    arc(s[2], 0, 2*s[2], 2*s[2], PI/2.0, PI);

    // styles for the squares
    noFill();
    stroke(255, 255, 255, 255);
    strokeWeight(1);

    // draw the square
    rect(0, 0, s[2], s[2]);

    // calculate the next number in the fibonacci sequence
    tmp = s[2];
    s[2] += s[1];
    s[0] = s[1];
    s[1] = tmp;

    // translate to get in position for the next square
    switch(phase % 4) {
      case 0:
        translate(s[1], 0);
      break;
      case 1:
        translate(-s[0], s[1]);
      break;
      case 2:
        translate(-s[2], -s[0]);
      break;
      case 3:
        translate(0, -s[2]);
      break;
    }

    phase++;
  }
}